Back to publication index
Bit Allocation for Wavelet Image Compression and Uniform Bit Loss
Alexander E. Mohr1
- Eve A. Riskin - Richard E. Ladner
Proceedings of the 32nd Annual Conference on Information Sciences
and Systems, March 1998 (CISS'98). 2 pages.
ps (217k) -
pdf (373k) -
ps.gz (42k) -
pdf.gz (80k) -
DOS-format ps (220k).
Abstract
We explore the distribution of bits among wavelet image subbands
that are transmitted across a channel with uniform bit loss, which models
interleaved data sent across a packet erasure channel.
We develop a closed-form expression
relating the source rate-distortion curves to the rate-distortion
curves that include the effect of expected bit losses. We use that
expression to determine optimal bit assignments for each subband.
Our results show that the bit allocation is biased against long codeword
indexes; as a result, the bit allocation is more uniform among subbands
in the
presence of loss than under conditions of no loss.
To demonstrate our methods, we use a 3-level discrete wavelet
transform and encode each subband with its own balanced tree-structured
vector quantizer of block size 2 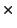 2.
2.
Approach
The wavelet transform is a linear orthonormal transform that
concentrates signal energy in a small number of subbands,
and any error introduced in the
transform domain is quantitively identical in the signal domain.
A tree-structured vector quantizer is progressive: a crude
representation is transmitted first, followed by better and better
approximations in subsequent passes.
Our approach to handling the loss of a
bit in a codeword is to truncate it to the previously-received bits, thus
treating those bits as an index to an internal node in the tree.
Adjusted Distortion
We derive an equation for the expected distortion in the
presence of bit loss, as seen by
the receiver.
- Let r be the rate in bits per vector.
- Let Dr be the distortion at rate r.
- Let PL be the probability of losing a bit.
We then let
be the probability
that bit k is ``useful,'' which we define as the case in
which that bit is received and the previous bit is also ``useful.''
Solving that recurrence yields:
The ``benefit'' of a bit is the decrease in distortion
that results from receiving that bit, as illustrated in
Figure 1:
Figure 1:
The ``benefit'' of a bit is the decrease in distortion
due to receiving that bit. It is a positive number.
![\includegraphics[width=0.49\textwidth]{benefit_example.eps}](img3.gif) |
In the presence of bit
loss, the k-th bit no longer reduces the distortion by Bk,
but rather by the smaller quantity
PU,k Bk. That change results
in the following equation for the adjusted distortion:
| D'r |
= |
 |
(4) |
In other words, the adjusted distortion for a given rate is the distortion
at rate 0 subtracted by the adjusted benefit of each additional
bit.
Bit Allocation
Figure 2:
As bit losses increase, fewer bits are assigned to the
low-frequency thumbnail subband, whereas more bits are
assigned to high-frequency detail subbands.
![\includegraphics[width=0.49\textwidth]{bit_allocation.eps}](img5.gif) |
Bit allocation among the subbands is done with an
extension [1] to the GBFOS
algorithm [2]. It allocates
bits among the various subbands such
that all allocations lie on the lower convex hull of the rate-distortion
curve. The effect of Equation 4 is to bias the
allocation against longer codeword indexes. As the percentage of lost
bits increases, the coarse subbands that would
normally have many bits assigned to them (corresponding to a deep
tree) end up with a reduced number of bits, while the fine-scale
subbands that would usually have few, if any, bits assigned to them,
end up receiving more (but still not as many as the coarse ones, as
shown in Figure 2). Essentially, in the presence of
high bit loss rates, the benefits of allocating bits to low-rate detail
subbands are diminished, but the benefits of high-rate coarse subbands are
diminished far more rapidly.
Conclusion
Bit loss reduces the slope of the rate-distortion curve by a
factor that is exponential in the bit rate. The exponential factor
implies that short
codeword indexes are affected less than long vector indexes.
As losses increase, an allocation that is skewed towards low frequency
subbands will shift to an allocation that is more evenly distributed.
It is interesting to note that a
scheme that equalizes the bit rate assigned to each subband would
largely eliminate the
tradeoff.
For example, using higher dimension vectors
for the fine-scale bands would collect the information content of
even more coefficients into a single codeword.
Future Work
In other work, we examine the effect of bit errors on the same
class of decompositions and develop methods to detect and correct those
errors. In future work, we will explore methods of using channel
coding to protect
state-of-the-art
image compression schemes, such as EZW [3] or
SPIHT [4], as they are sent across lossy channels.
- 1
-
E. A. Riskin, ``Optimum bit allocation via the generalized BFOS algorithm,''
IEEE Transactions on Information Theory, vol. 37, pp. 400-402, Mar.
1991.
- 2
-
L. Breiman, J. H. Friedman, R. A. Olshen, and C. J. Stone, Classification
and Regression Trees.
The Wadsworth Statistics/Probability Series, Belmont, California:
Wadsworth, 1984.
- 3
-
J. M. Shapiro, ``Embedded image coding using zerotrees of wavelet
coefficients,'' IEEE Transactions on Signal Processing, vol. 41,
pp. 3445-3462, Dec. 1993.
- 4
-
A. Said and W. A. Pearlman, ``A new, fast, and efficient image codec based on
set partitioning in hierarchical trees,'' IEEE Transactions on Circuits
and Systems for Video Technology, vol. 6, pp. 243-250, June 1996.
Footnotes
- ... Mohr1
-
This work was supported by U.S. Army Research Office
grant DAAH04-96-1-0255, an NSF Young Investigator Award, and a Sloan
Research Fellowship.
Departments of Electrical Engineering and Computer Science and Engineering,
University of Washington, Box 352500, Seattle, WA 98195-2500. http://rcs.ee.washington.edu/dcl/amohr/
Alex Mohr
1998-11-16
![\includegraphics[width=0.49\textwidth]{benefit_example.eps}](img3.gif)
![\includegraphics[width=0.49\textwidth]{benefit_example.eps}](img3.gif)
![\includegraphics[width=0.49\textwidth]{bit_allocation.eps}](img5.gif)