Graceful Degradation over Packet Erasure Channels through Forward
Error Correction
| Alexander E. Mohr | Eve A. Riskin | Richard E. Ladner
* |
| Computer Sci. and Engr. | Electrical Engineering | Computer Sci. and Engr. |
| University of Washington | University of Washington | University of Washington |
| Seattle, WA 98195–2350 | Seattle, WA 98195–2500 | Seattle, WA 98195–2350 |
| [email protected] | [email protected] | [email protected] |
|
PDF version or publication list
Abstract
We present an algorithm that assigns unequal
amounts of forward error correction to progressive data
so as to provide graceful degradation of image quality
as packet losses increase.
We use the SPIHT coder to compress images in this work, but our
algorithm can protect any progressive compression
scheme. The algorithm can also use almost any
function as a model of packet loss conditions.
We find that for an exponential packet loss model with a mean of 20%
and a total rate of 0.2 bpp,
good image quality can be obtained, even when 40% of transmitted packets
are lost.
1 Introduction
The Internet is a widely deployed network of computers that allows
the exchange of data packets. In traversing the network, a packet
is sent from computer to computer until it arrives at its destination.
Because of congestion, however,
packets are often discarded, causing loss of data and most likely
decoding failure if the lost data are not replaced.
When each packet is assigned a unique sequence number, it is
known which packets are received and which are lost. If the underlying
transport protocol does not assign a sequence number, one or two bytes
of the payload can be used to provide one.
The sequence number allows the receiver to sort the
packets according to their
transmission order: any gaps in the sequence are known to be
lost packets and out-of-order packets can be positioned correctly.
The receiver takes whatever action it deems
best to decode the data.
In networks in which packets are discarded at random, there is
no way to specify the importance of a particular packet. However,
the data that we transmit usually vary in importance.
If we transmit a portrait of a face, for example,
data that let us recognize the person are more important
than data that show the texture of a few strands of hair. If the
network is unable to transmit all of the data, then
we would like it to discard the part describing the hair and retain
the part that allows recognition of the face.
Such a coding strategy needs
to quantify the importance of different chunks of data and protect
important data more than it protects less-important data.
A compression algorithm that provides a progressive
ordering of the data will enable us to determine which
data are most important to the signal quality.
In this paper, we describe an algorithm to assign unequal amounts of
forward error correction (FEC)
to images that are first compressed with an unmodified progressive algorithm
(such as SPIHT [1]) and then
transmitted over lossy packet networks.
Our scheme is modular in
that we can use any progressive
compression algorithm and have
graceful degradation with increasing packet loss rate.
We focus on those channels without feedback
whose variable loss rates
can be
modeled
by a probability mass function (PMF). Notable examples are
Asynchronous Transfer Mode (ATM) networks and
UDP-based transport on the Internet.
1.1 Set Partitioning in Hierarchical Trees
An example of a progressive image compression algorithm is
SPIHT
[1].
This algorithm is an extension of Shapiro's Embedded
Zerotree Wavelet algorithm [2].
These two new algorithms are a significant breakthrough in lossy image
compression in that they
give substantially higher compression ratios
than prior lossy compression
techniques including JPEG [3],
vector quantization [4], and
the discrete wavelet transform
[5] combined with quantization.
In addition, the algorithms allow for progressive transmission [6]
(meaning coarse approximations
of an image can be reconstructed quickly from
beginning parts of the bitstream),
require no training, and
are of low computational complexity.
1.2 Joint Source/Channel Coding Using SPIHT
Joint source/channel coding is an area that has attracted
a significant amount of research effort.
Despite the fact that Shannon's separation theorem [7]
states that for a
noisy channel, the source
and channel coders can be independently designed
and cascaded with the same results as given by a joint
source/channel coder,
complexity considerations have led
numerous researchers
develop joint source/channel coding techniques
[8, 9].
To date, a majority of this effort has been for fixed rate
codes because they do not suffer from the synchronization problems
that occur with variable rate codes.
(Notable exceptions that have considered joint
source/channel coding schemes for variable rate codes
include work on reversible variable length codes
that can be decoded in both directions [10].
However, these codes can still have problems with synchronization.)
SPIHT has the advantage of yielding
impressive compression ratios for still images,
but
images compressed with SPIHT are vulnerable
to data loss.
Furthermore, because
SPIHT produces an embedded or progressive bitstream, meaning that
the later bits in the bitstream refine earlier
bits, the earlier bits are needed for the
later bits to even be useful.
However, SPIHT's excellent compression performance
is leading researchers to consider the problem of
transmitting images compressed
with SPIHT over lossy channels and networks.
1.3 Prior Work on Transmitting SPIHT Over Lossy Channels
Sherwood and Zeger [11] protected
images compressed with SPIHT against noise from the memoryless
binary symmetric
channel with RCPC codes [12] with good
results. They extended this work to images
transmitted over the Gilbert-Elliott channel (a fading
channel) in [13].
In the latter case, they implement a product code of RCPC
and Reed-Solomon codes and find that this outperforms the
work in [11] even for the binary symmetric channel.
Rogers and Cosman [14] used a fixed-length packetization
scheme called packetized
zerotree wavelet (PZW)
compression to transmit images compressed with a modified SPIHT
over lossy packet networks.
The algorithm does not use any channel coding,
and hence can be considered joint source/channel coding.
They implemented a scheme to fit as many complete wavelet trees
(i.e. one coefficient from the lowest frequency wavelet subband along with
all its descendants) as possible into a packet.
The algorithm degrades gracefully in the
presence of packet loss because the packets are independent.
If a packet is lost, they attempt to reconstruct
the lowest frequency coefficients from the
missing trees of wavelet coefficients by interpolating from
neighboring low frequency coefficients that have been
correctly received by the decoder.
To simplify their algorithm, they used fewer levels of
wavelet decomposition and
removed the arithmetic coder from the SPIHT algorithm.
The modification of the SPIHT algorithm caused a decrease
of about 1.1 dB in the
PSNR at 0.209 bits per pixel
for the case of a channel without losses.
These two schemes were combined into a hybrid
scheme in [15].
The authors consider the case where, in addition to packet loss,
packets can arrive with bit errors in them.
They use channel coding to correct bit errors
and PZW to conceal
packet losses.
If they can not correct
all of the bit errors in a packet, they
consider the packet to be erased.
The hybrid scheme shows resilience to
packet loss, bit errors, and error bursts. It is still
based on the modified SPIHT algorithm used in
[14], which does not perform as well as the original
SPIHT algorithm.
1.4 Forward Error Correction for Packet Erasure Channels
Priority Encoding Transmission (PET)
[16]
is an algorithm that assigns FEC, according to priorities
specified by the user,
to message fragments (also specified by the user)
sent over lossy packet networks.
Each of these fragments is protected from packet erasures by added FEC.
Priorities can range from high, which means that the message
fragment can be recovered if relatively few packets
are received by the decoder, to low, meaning that most or all
packets need to be received to recover the message fragment.
This recovery is possible by treating the message fragment as the
coefficients of a polynomial in a Galois field and evaluating it
at a number of additional points, thus creating redundant
data [17].
The receiver can recover the message fragment by interpolation from
any subset of the transmitted packets, so long as it receives
a fraction of packets at least as large as the priority of
the message fragment.
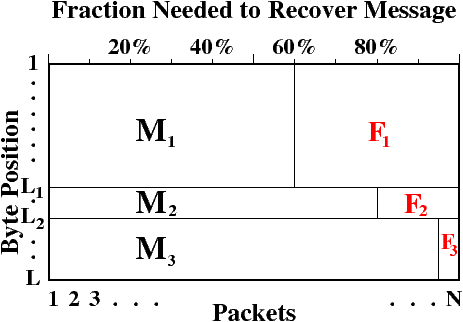
| Figure 1: In Leicher's application of PET to MPEG.
he applied 60% priority to message fragment M1
(the I frames), 80% priority
to M2 (the P frames), and 95% priority to M3 (the B frames).
Each message and its associated FEC use the same range of bytes
in every packet. |
In the PET algorithm,
each message fragment is assigned a fixed position within each
packet. For figure 1, the first fragment
M1 and its FEC F1 consist of the first L1 bytes
of each packet, the second fragment M2 and its FEC F2
consist of bytes from
(L1+1) to (L2)
of each packet, and M3 and F3 consist of the remaining
bytes of each packet.
PET determines the value of Li for each fragment and the total
number of packets N, making the
assumption that the number of fragments is much smaller than the number
of bytes in each packet, and constrained by the user-specified priorities.
The PET algorithm does not specify how to choose the
priorities to assign to the various message fragments:
this assignment is left to the user.
It defines priorities as the fraction of transmitted
packets that must be received to decode the message; thus a high
priority is represented by a low percentage.
Leicher [18] applied PET to video compressed
with MPEG and transmitted over
packet loss channels. He used a simple three-class system in which
M1 was the intraframe (I) frames and had priority 60%,
M2 was the forward-only predicted (P) frames and had priority 80%,
and M3 was the forward-backward predicted (B) frames and had
priority 95%.
Thus, he can recover the I frames from 60% of the packets,
the I and P frames from 80% of the packets,
and all the data from 95% of the packets.
This is diagrammed in Figure 1.
In related work, Davis, Danskin, and Song [19] presented
fast lossy Internet image transmission (FLIIT)
which is a joint source/channel coding algorithm that,
like PET, assigns different levels of FEC to different types of data,
but it considers distortion-rate tradeoffs in its assignments.
They begin with a 5-level discrete wavelet transform,
create an embedded bitstream by quantizing each subband's
coefficients in bit planes, apply entropy coding, and
pack the bitstream from each subband into 64-byte blocks.
To do bit allocation, they determine the reduction
in distortion due to each block, similar to work in
[20].
They then compare the greatest decrease in distortion from
those blocks with the addition of a block of FEC data to the
already-allocated blocks. They
allocate the block of data or block of FEC that decreases
the expected distortion the most.
They only consider three simple cases
of assigning FEC to a block: no protection, protection
that consists of one FEC block shared among a group of
blocks, and replication of the block.
They find that, as expected, it is advantageous to apply
more FEC to the coarse/low frequency wavelet scales and to the
most significant bit planes of the quantization.
2 An Algorithm for Assigning Forward Error Correction
While the algorithms in
[13, 14, 15, 19]
yield good results for
memoryless and fading channels and for lossy packet
networks, there are additional ways to transmit compressed images
over lossy networks such that image quality
gracefully degrades with increasing packet loss.
Specifically, we will protect images
transmitted over lossy channels with unequal amounts of FEC
in a manner similar
to the PET scheme, but we will consider the
increase in PSNR due to each data byte when assigning our
protection.
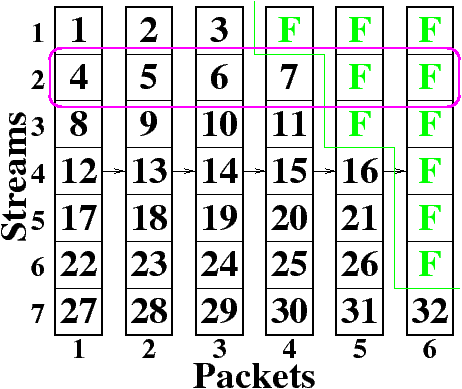
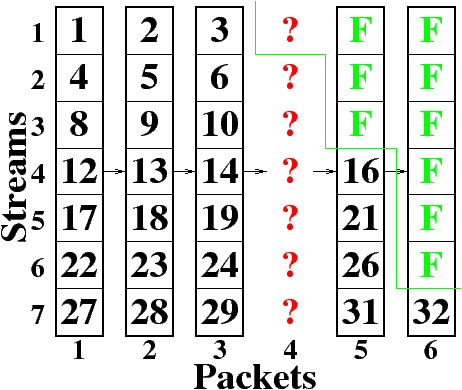
| Figure 2: Each of the rows is a stream and each of the
columns is a packet. A stream
contains one byte from each packet. Here, a message of 32 bytes of
data (numbers 1-32) and ten bytes of FEC (F)
is divided into seven streams and sent in six packets. |
In our approach to using PET to assign unequal amounts
of FEC to progressive data, we remove PET's restriction that the number
of message fragments be much less than the number of bytes in
each packet.
Instead, we use a number of message fragments equal to the
number of available bytes in each packet and have
our algorithm dynamically choose
the length and content of each message fragment.
We add FEC
to each message fragment
to protect against packet loss such that
the fragment and the FEC form a stream.
The message is divided into L streams such that
each stream has one byte of each of N packets.
In Figure 2, each of the L=7 rows is a stream and each
of the N=6
columns is a packet.
For a given stream i, for i=1,2,…,L, containing both data bytes
and FEC bytes, as long as the number of lost packets is
less than or equal to the number of FEC bytes,
the entire stream can be decoded [16].
Figure 2 shows one possible way to send a message
of 32 bytes of
data (numbers 1-32) and ten bytes of FEC (F).
Notice that in the figure, more bytes of FEC are applied to the
earlier parts of the message and fewer are used for the
later parts of the message. For SPIHT, which produces an embedded bitstream,
the earlier parts of the message should have the highest priority
because they are most important to the overall quality of the
reproduction.
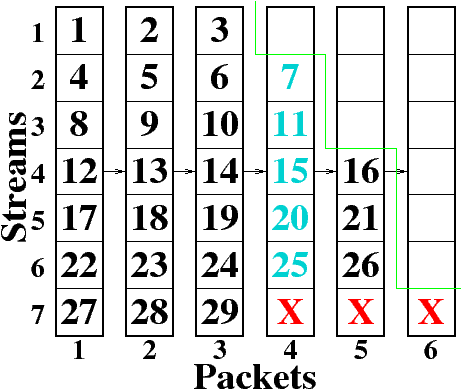
| Figure 3: Demonstration of how much data can be recovered
when one of six packets is lost. Here, stream one is unaffected
by the loss, streams two through five use FEC to recover from the
loss, and in stream seven, only the bytes up to the lost packet
are useful to the decoder. |
Figure 3 shows
the case where one packet out of six is lost, and five are
received correctly.
In this case, the first six streams can be recovered
since they contain five or fewer data bytes.
The last stream can not be decoded since it contains
six bytes of data and no FEC.
We point out that
bytes 27-29 from the seventh stream are useful since
they were received correctly, but for an embedded bitstream,
bytes 31 and 32 are not useful without byte 30.
Similarly, if two packets are lost, bytes 1-11 are
guaranteed to be recovered and bytes 12-15 may or may not be
recovered. In messages of practical length, however, those
few extra bytes have only a small effect on image
quality.
Analogous to progressive transmission
[6], even if severe packet loss occurred,
we could recover a lower fidelity
version of the image from the earlier streams
that are decoded correctly.
Each additional stream that is successfully decoded
improves the quality of the received message, as long as
all previous streams are correctly decoded.
2.1 Notation
Assume we have a message M, which is simply a sequence of data bytes
to be transmitted.
For example, this could be a still image compressed with SPIHT to 0.5 bits
per pixel.
If, instead of sending M, we send a prefix of M and some FEC,
we can still maintain the same overall bit rate.
We let mi equal the number of data bytes
assigned to stream i and let
fi = N−mi equal the number of FEC bytes
assigned to stream i.
We define an L-dimensional
FEC vector whose entries are the
length of FEC assigned to each stream as:
For a given f, we
divide M into fragments Mi(f) and define
Mi(f) to be the sequence of data bytes in the ith
stream. That is, Mi(f) includes the bytes of message M
from position ∑j=1i−1 mj + 1 to position ∑j=1i mj;
i=2,3,…,L, with M1(f) composed of m1 bytes of
stream 1.
We denote a prefix
of M containing the first j fragments for redundancy vector f
as:
| M(j, f) = M1(f) M2(f) … Mj(f). |
We now introduce the incremental PSNR of stream i:
| gi(f) = PSNR[M(i, f)]
− PSNR[M(i−1, f)]. |
The quantity gi(f) is the amount by
which the PSNR increases when the receiver
decodes fragment i, given that all fragments prior
to i have already been
decoded. We set
g1(f) to be the difference in PSNR between the case in which
M1(f) is received and the case in which no information is received.
Because the data are progressive,
we require that fi ≥ fi+1; i=1,2,…,L−1;
that is, the FEC assigned to the streams
is non-increasing with i.
With this requirement, if Mi(f) can be decoded, then
M1(f),M2(f),…,Mi−1(f)
can also be decoded.
The packet loss model we use is given by a PMF pn; n=0,1,…,N,
such that pn is the probability that n packets are lost. To
simplify calculations, we determine the probability that k or
fewer packets are lost, and thus
the CDF is c(k) = ∑n=0k pn; k=0,1,…,N. The
quantity c(fi) is the probability that receiver can decode
stream i.
We can now calculate the expected PSNR of the received message
as a function of
f by summing over the L streams:
In designing our algorithm to assign FEC,
we seek the
f that maximizes G(f)
subject to our packet loss model pn.
2.2 Channel Loss Model
To determine the FEC vector f, we need an estimate
of the channel loss model pn that a message is likely to encounter.
In keeping with our modular design philosophy, we assume that
channel loss behavior can be modeled by an estimator
that outputs a PMF that
indicates the likelihood that a particular number of packets is
lost.
How the estimator derives its estimate of current channel conditions
is not addressed by this paper.
2.3 The Algorithm
Finding the globally optimal
assignment of FEC data to each stream is computationally
prohibitive for a useful amount of data.
We therefore developed a hill-climbing algorithm that makes
limited assumptions
about the data, but is computationally tractable.
As mentioned in Section 2.1,
we constrain fi ≥ fi+1.
Additionally, we assume that
a single byte missing from the progressive bitstream causes all later bytes
to become useless.
Finally, the PMF should be reasonably well-behaved: the more it
deviates from a unimodal function, the larger the search distance
must be to capture the irregularities.
| Figure 4: At each iteration of the optimization algorithm,
Q bytes of data can be added or subtracted to any of the L
streams. |
We initialize each stream to contain only data bytes,
such that mi = N and fi = 0; i=1,2,…,L.
In each iteration, our algorithm
examines a number of possible assignments equal to 2QL, where
Q is the search distance
(maximum number of FEC bytes that can
be added or subtracted
to a stream in one iteration) and L is the
number of streams.
We determine G(f) after adding
or subtracting 1 to Q bytes of FEC data to each stream
(see Figure 4),
while satisfying our constraint fi ≥ fi+1.
We choose the f corresponding to the highest G(f),
update the allocation
of FEC data to all affected streams,
and repeat the search until none of the cases examined improves
the expected PSNR.
This algorithm will find a local maximum that we believe
is quite close to the global maximum and, in some cases, may
be identical to the global maximum.
Note that for every byte of FEC data
that we add to a stream, one byte of data needs to be removed.
When changing the FEC assignment, we start at the
first stream affected by the new allocation, move
its last data byte to the next stream,
move the last data byte of this stream to the next
stream, and so on.
This causes a cascade of data bytes to move down the streams until the
last data byte from stream L is discarded. This part of
the algorithm makes use
of our assumption that the compressed sequence is progressive,
because the data byte that we discard is among the least important
in the embedded bitstream.
3 Results
For these experiments, we used
the standard 512 × 512 gray-scale Lenna image
compressed with SPIHT.
We chose a total bit rate of 0.2 bits per pixel
for the combination of data and FEC bytes and
used an exponential packet loss model with a mean loss rate of 20%.
Because ATM packets have a payload length of 48 bytes and one
byte is required for a sequence number, we place 47 bytes
of data in each packet and send 137 packets, giving a total
payload size of 6576 bytes, of which 6439 are data. Including
the sequence number, the bit rate is 0.201 bits
per pixel. Excluding it, the bit rate is 0.197 bits
per pixel.
Convergence of the algorithm is typically reached in about
27 iterations
and requires 7.3 seconds of CPU time on a Sun SPARCstation 10 workstation
or 0.5 seconds
on an Intel Pentium II 300MHz workstation.
We had our algorithm maximize expected PSNR for two cases:
unequal erasure
protection, in which the algorithm could freely allocate FEC to
the compressed data; and equal erasure protection, in which
the algorithm was constrained to assign FEC equally among all
of the streams.
For unequal assignment,
the result was an allocation with an expected PSNR
of 29.42 dB.
For equal assignment,
the result was an allocation with
an expected PSNR of 28.94 dB,
or 0.48 dB lower than the unequal assignment result.
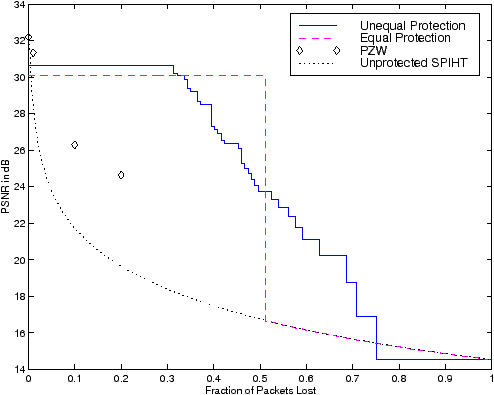
| Figure 5: Effect of packet loss on PSNR for
unequal erasure protection,
equal erasure protection,
Rogers and Cosman's PZW,
and unprotected SPIHT. The two erasure protection results are
from an exponential packet loss model with a mean loss rate of 20%. |
As shown in Figure 5, under good channel conditions
(erasure rates of up to 32%, which occur 80% of the time)
unequal erasure protection yields a PSNR
that is 0.66 dB higher
than equal erasure protection.
This is because
more bytes are used for data and fewer for
FEC.
Equal erasure protection does surpass
unequal erasure protection
when
loss rates are 33% to 51%, but those occur with only 11% probability.
In addition, unequal erasure protection degrades gracefully whereas
equal erasure protection has a sharp transition at
loss rates near 51%.
As expected, both of these
cases substantially outperform not using any protection on the data,
except when the loss rate is very low.
At those low loss rates, e.g. below 1-2%, unprotected SPIHT
will often survive with a significant prefix of the transmitted
data remaining intact, and the more-robust PZW coder [14] will
perform slightly better. On the other hand, their performance degrades
rapidly as losses increase, while the addition of FEC allows
protected data to survive at larger loss rates. We also note
that the protected data is affected only by the number of
lost packets, but the reconstruction quality of unprotected
SPIHT, and to a lesser extent PZW, depends upon which packets
are lost.
| Figure 6: Image quality at 0.2 bpp total rate for
unequal erasure protection on a channel with
an exponential loss model that
averages 20%. Loss rates from left to right: 30%,
40%, 50%, and 60%. |
We display results of using unequal erasure protection in
Figure 6. It shows the graceful degradation
of the image transmitted over a lossy
packet network with loss rates of 30%, 40%, 50%, and 60%.
Notice that the image quality remains high at a loss rate of
40% and the image is still recognizable at a loss rate of 50%.
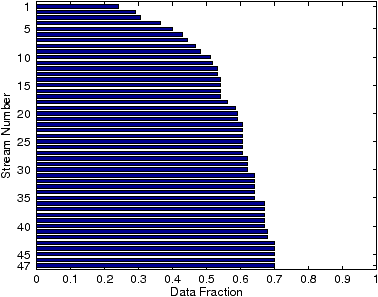
| Figure 7: Data fraction for each
stream. Note that the FEC fraction is (1 - Data Fraction).
Stream 1 is the first stream (most important
data) and stream 47 is the last stream (least important
data). |
Finally, we show how the algorithm assigns data and
FEC to the different data streams
for the Lenna image compressed with the SPIHT algorithm
in Figure 7.
Stream 1 is the first stream (most important
data from the SPIHT algorithm) and it has an assignment of 24%
data and 76% FEC. Stream 47 is the last stream (least
important data) with 70% data and only 30% FEC.
As expected, the amount of FEC decreases with
increasing stream number, as required by our algorithm.
4 Conclusion
We have developed an algorithm that determines the
amount of FEC to assign to data from SPIHT
to provide graceful degradation in the case of packet loss.
Our algorithm is modular and can input any compression
scheme that produces a progressive bitstream.
Future work will include
allowing more constraints such as specifying a minimum usable PSNR,
speeding up the FEC
assignment algorithm so that it can be recalculated in real-time,
and
applying it
to other progressive compression algorithms for images and
video.
The authors would like to thank
Gary W. Garrabrant for helpful discussions about
lossy packet networks, and Professor William Pearlman
for the SPIHT source code.
Demo programs and data files
can be found at
http://isdl.ee.washington.edu/compression/amohr/uep/.
References
-
[1]
-
A. Said and W. A. Pearlman, “A new, fast, and efficient image codec based on
set partitioning in hierarchical trees,” IEEE Transactions on Circuits
and Systems for Video Technology, vol. 6, pp. 243–250, June 1996.
- [2]
-
J. M. Shapiro, “Embedded image coding using zerotrees of wavelet
coefficients,” IEEE Transactions on Signal Processing, vol. 41,
pp. 3445–3462, Dec. 1993.
- [3]
-
W. B. Pennebaker and J. L. Mitchell, JPEG: Still Image Data Compression
Standard.
New York: Van Nostrand Reinhold, 1993.
- [4]
-
A. Gersho and R. M. Gray, Vector Quantization and Signal Compression.
Boston: Kluwer Academic Publishers, 1992.
- [5]
-
M. Antonini, M. Barlaud, P. Mathieu, and I. Daubechies, “Image coding using
wavelet transform,” IEEE Transactions on Image Processing, vol. 1,
pp. 205–220, Apr. 1992.
- [6]
-
K. Tzou, “Progressive image transmission: a review and comparison of
techniques,” Optical Engineering, vol. 26, pp. 581–589, July 1987.
- [7]
-
C. E. Shannon, “A mathematical theory of communication,” Bell Systems
Technical Journal, vol. 27, pp. 379–423, 1948.
- [8]
-
N. Farvardin, “A study of vector quantization for noisy channels,” IEEE
Transactions on Information Theory, vol. 36, pp. 799–809, July 1990.
- [9]
-
R.-Y. Wang, E. A. Riskin, and R. Ladner, “Codebook organization to enhance
maximum a priori detection of progressive transmission of vector quantized
images over noisy channels,” IEEE Transactions on Image Processing,
vol. 5, pp. 37–48, Jan. 1996.
- [10]
-
J. Wen and J. D. Villasenor, “Reversible variable length codes for efficient
and robust image and video coding,” in Proceedings Data Compression
Conference, pp. 471–480, March-April 1998.
- [11]
-
P. G. Sherwood and K. Zeger, “Progressive image coding for noisy channels,”
IEEE Signal Processing Letters, vol. 4, pp. 189–191, July 1997.
- [12]
-
J. Hagenauer, “Rate-compatible punctured convolutional codes (RCPC
Codes) and their applications,” IEEE Transactions on Communications,
vol. 36, pp. 389–400, Apr. 1988.
- [13]
-
P. G. Sherwood and K. Zeger, “Error protection for progressive image
transmission over memoryless and fading channels,” IEEE Transactions on
Communications, 1998.
Accepted for publication.
- [14]
-
J. K. Rogers and P. C. Cosman, “Robust wavelet zerotree image compression with
fixed-length packetization,” in Proceedings Data Compression
Conference, pp. 418–427, March-April 1998.
- [15]
-
P. C. Cosman, J. K. Rogers, P. G. Sherwood, and K. Zeger, “Combined forward
error control and packetized zerotree wavelet encoding for transmission of
images over varying channels,” IEEE Transactions on Image Processing,
1998.
To appear.
- [16]
-
A. Albanese, J. Blömer, J. Edmonds, M. Luby, and M. Sudan, “Priority
encoding transmission,” IEEE Transactions on Information Theory,
vol. 42, pp. 1737–1744, Nov. 1996.
- [17]
-
L. Rizzo, “Effective erasure codes for reliable computer communication
protocols,” ACM Computer Communication Review, vol. 27, pp. 24–36,
Apr. 1997.
- [18]
-
C. Leicher, “Hierarchical encoding of MPEG sequences using priority
encoding transmission (PET),” Tech. Rep. TR-94-058, ICSI, Nov. 1994.
- [19]
-
G. M. Davis, J. M. Danskin, and X. Song, “Joint source and channel coding for
Internet image transmission,” in Proceedings of ICIP, vol. 1,
pp. 21–24, Sept. 1996.
- [20]
-
Y. Shoham and A. Gersho, “Efficient bit allocation for an arbitrary set of
quantizers,” IEEE Transactions on Acoustics Speech and Signal
Processing, vol. 36, pp. 1445 – 1453, Sept. 1988.